Question
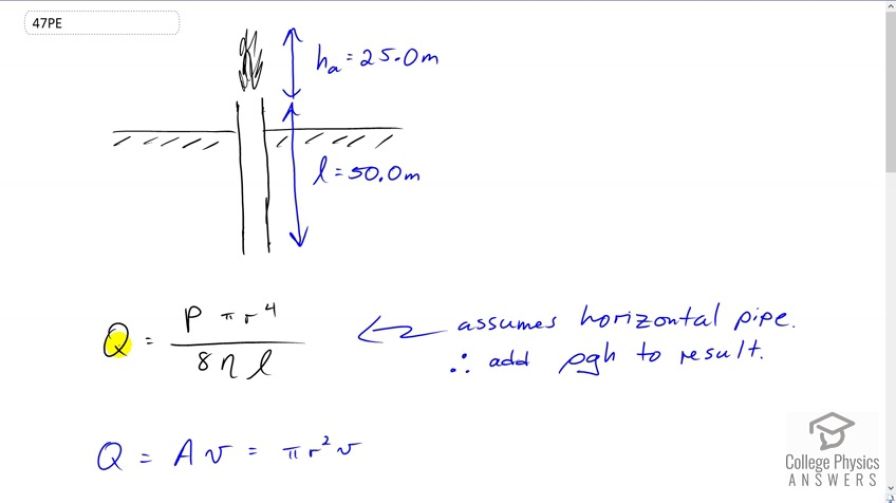
An oil gusher shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. Neglecting air resistance but not the resistance of the pipe, and assuming laminar flow, calculate the gauge pressure at the entrance of the 50.0-m- long vertical pipe. Take the density of the oil to be and its viscosity to be (or ). Note that you must take into account the pressure due to the 50.0-m column of oil in the pipe.
Final Answer
Solution video
OpenStax College Physics, Chapter 12, Problem 47 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have this formula which is the Poiseuilles Law that tells us the flow rate though a pipe but it assumes that the pipe is horizontal. So we can use this still to get an answer despite the fact that this pipe here is vertical. But when we get an answer we'll have to add the pressure due to this column of oil in the pipe to our answer that we get from this formula. So we also know that the volume flow rate through this pipe is going to be its cross-sectional area times the speed of the oil going through it. Now I guess we should talk about this picture a little bit. We have this oil pipe in the ground and the pipe we're told has a length of 50 meters and the oil gushes out the top to a height of 25 meters. It stops at the very top there, of course. So we want to substitute for v because we don't really know what v is. But we know from this kinematics formula the final speed squared equals initial speed squared plus two times acceleration times displacement. Final speed is zero and then we can solve for initial speed which is the speed at the mouth of the pipe here which is this v here. We can subtract two a d from both sides and then switch the sides around to get v i on the left and then take the square root of both sides. So it's the square of negative two a d. Now the acceleration is negative g and so we end up with a positive under the square root and this displacement is this height a, height in the air, height above the mouth of the pipe which is 25 meters. So we substitute that in for v in our formula for the volume flow rate and we also equate this with this. This is what we do here. So we have Poiseuilles' Law on the left and on the right hand side we have this you know, equation of continuity I think they call it. It's volume flow rate being the cross-sectional area times the speed of the fluid. Now we have to solve for p. So the pi cancels, and when we divide r squared by r to the power four we end up with r squared in the denominator. Then we multiply both sides by eight nu l and we end up with this expression here. So we plug in numbers and we get eight times square root of two times 9.81 meters per second squared, times 25 meters height from the mouth of the pipe to the top of its path in the air, times one pascal second for viscosity, times 50 meter length of the pipe, divided by the pipe's radius which is its diameter divided by two, so 0.1 meters over two, and we square that. We get 3.5436 times ten to the six pascals. Now because this pipe is vertical we have to add to that the pressure due to the height of the column of oil. So that's this answer from before plus 900 kilograms per cubic meter density of oil, times 9.81 newtons per kilograms, times 50 meter length pf the pipe, which gives 3.99 times ten to the six pascals is the gauge pressure at the very bottom.
Comments
Hello,
In this equation, why is pressure due to weight of the fluid added to, rather than subtracted from, the pressure difference indicated by Poiseulle's Law? Since presumably the pressure will be greatest at the base of the pipe, I thought that it would contribute to the pressure difference along it? Is the pressure due to weight of the fluid resisting the flow of the oil out of the pipe? I am just confused here, since I didn't think that pressures had any direction due to being a scalar quantity, but in this case it seems that we take the direction of the pressure due to weight to be only downward, and thus it resists the flow out of the pipe.

