Question
A skydiver will reach a terminal velocity when the air drag equals their weight. For a skydiver with high speed and a large body, turbulence is a factor. The drag force then is approximately proportional to the square of the velocity.
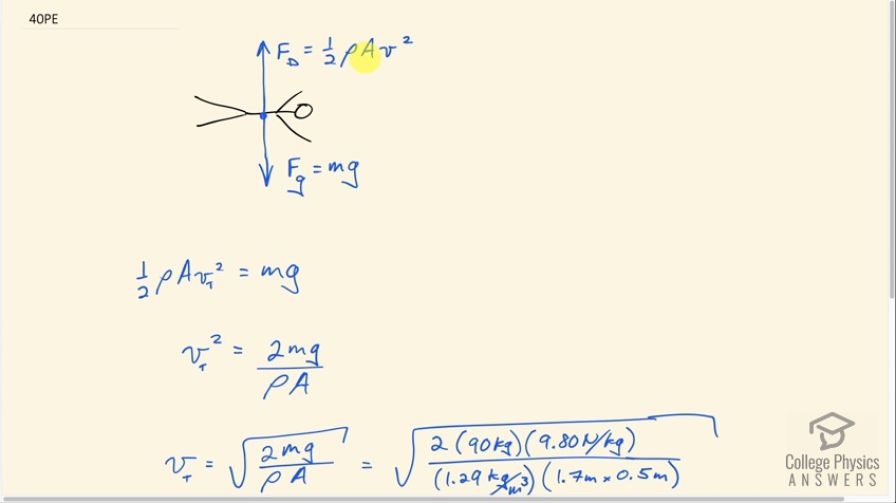
Taking the drag force to be and setting this
equal to the person’s weight, find the terminal speed for a person falling “spread eagle.” Find both a formula and a number for , with assumptions as to size.
Final Answer
Solution video
OpenStax College Physics, Chapter 12, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When a skydiver is falling spread eagle, the drag force will have a formula one half times the density of air times, the cross-sectional area of the person and multiply by their speed squared. Now, the area is this area that's if you were to be a person standing on the ground and looking straight up. And you're looking upwards. Use your eye, Paul. Funny picture. Anyway, looking upwards. This is the area that you would see blocking your view of the sky. So that's the area that's here. Okay. Or if the sun was shining straight down, would be the area of the shadow cast on the ground. All right, so there's terminal velocity happens when there's drag force upwards equals the weight downwards. So its one half rho A v t squared equals m g. That's when you have terminal velocity because there's no acceleration anymore. There's no net force. And so this is the maximum possible speed. So we're going to solve here v t by multiplying both sides by two over density times area. And we have v t squared equals two m g over rho times A and then we took square root of both sides to solve for terminal velocity. So that's the square root of two times the the person's mass times g divided by air density times the person's area. So the square root of two times 90 kilograms say, times 9.8 newtons per kilogram, divided by 1.29 kilograms cubic meter density of air, and multiply by 1.7 meters tall by 0.5 meters wide. Just assumptions of the size of their body. And then her terminal velocity would be 40 meters per second.
