Question
Show that the Reynolds number is unitless by substituting units for all the quantities in its definition and cancelling.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 12, Problem 52 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
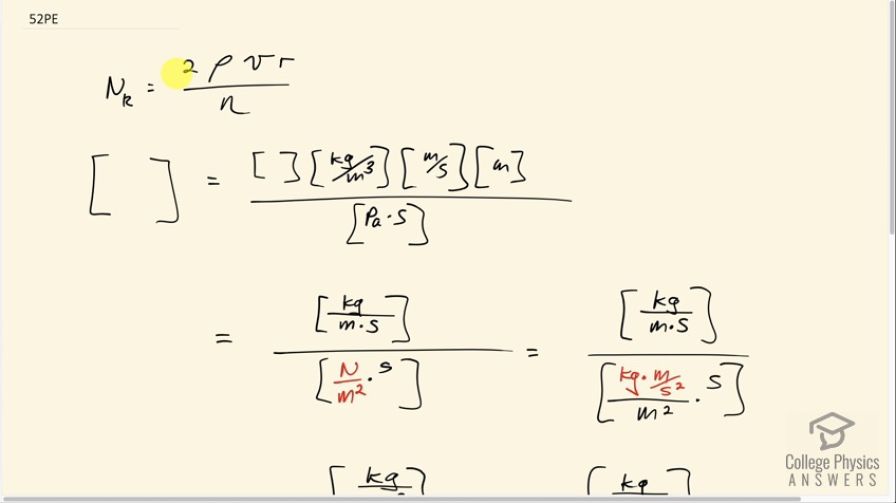
This is College Physics Answers with Shaun Dychko. We're going to show that the units of Reynold’s number is dimensionless. There are no units. And so we have the formula two times density of the fluid times its speed times the radius of the tube it's going through divided by the viscosity of the fluid. We're gonna substitute in the units for each of these factors and then see that they'll all cancel. So density has unit of kilogram per cubic meter, the number two has no units. Speed has units of meters per second, radius has units of meters and viscosity has units of Pascal seconds. So we take this numerator and multiply through. So, we have kilogram per cubic meter times meters per second and times meters again. So that's meters squared in the numerator of this portion that we're looking at and divided by meters cubed times seconds in the denominator of this top portion here. And this works out to kilograms per meter second. And then in the bottom, I made a substitution for pascals and wrote it as newtons per square meter, and then Newton can in turn be substituted with kilograms times meters per second squared. Because, you know, newtons second law is a force, which is Newton is mass times acceleration. So that mass is kilogram and acceleration is meters per second squared for units. And then we multiply the seconds by this numerator here and in this seconds and squared and then denominator of the numerator, which is kind of confusing. But I hope you can follow based on where this little yellow bubble is. This second here and the second squared and the bottom there will make seconds to the power of one. And then taking all of this and dividing by meter squared is the same as multiplying by the reciprocal of the denominator. So I just find it easier to look at it that way. So I'm going to multiply by one over a meter squared. And we see that this meter cancels with one of the meters here, leaving us with kilograms per meter second at the bottom and the units in the top are the same as units in the bottoms. They in turn cancel giving us no units in the end. Quod erat demonstrandum.