Question
The pressure drop along a length of artery is 100 Pa, the radius is 10 mm, and the flow is laminar. The average speed of the blood is 15 mm/s. (a) What is the net force on the blood in this section of artery? (b) What is the power expended maintaining the flow?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 0.031 N0.031 \textrm{ N}
  2. 4.7×10−4 W4.7\times 10^{-4}\textrm{ W}

Solution video

OpenStax College Physics, Chapter 12, Problem 32 (Problems & Exercises)

OpenStax College Physics, Chapter 12, Problem 32 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

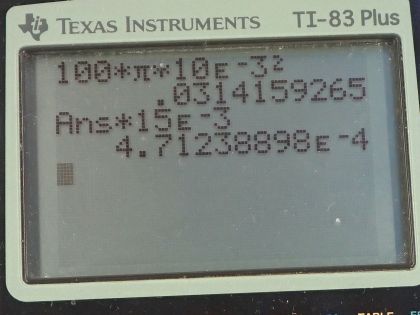
Calculator Screenshots

  • OpenStax College Physics, Chapter 12, Problem 32 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a section of artery with a radius of 10 millimeters that has a pressure drop across a certain section of 100 pascals. And the speed of blood through this section is 15 millimeters per second. And we convert that into 15 times 10 to the minus three meters per second. The radius is converted into meters as well by multiplying by 10 to the minus three. Since that's what the prefix ‘milla’ means. And I also wrote down the viscosity of blood at body temperature 37 degrees Celsius, thinking that that would be needed since I imagined we would use Poiseuille’s law when I first looked at the question, but it turns out it's simpler than that. In part A, we are asked to figure out what forces responsible for pushing the blood through this section of blood vessel. And the pressure difference is that net force divided by the cross sectional area of the blood vessel. And we can multiply both sides by A to solve for F net. So the net force then is the pressure difference times area, which is pi r squared, since it's a capillary or artery and which has a circular cross-section of area pi r squared. And so that's 100 pascals times pi times 10 times 10 to the minus three meters squared, which is 0.031 newtons. Then to find the power. We figure out the work done by the force, which is force times distance and divide that by time, but distance divided by time is the speed. So maybe that should be in red there, substitutions are in red. So we have force then that we found in part A multiplied by the speed of the blood 15 times 10 to the minus three meters per second. And that gives the power of 4.7 times 10 to the minus four watts.

Comments

Submitted by ts on Thu, 02/18/2021 - 18:50

link

Hello,

In this solution, I notice that when I use the power equation given in the textbook (P+1/2pv2+pgh)Q=powerP + 1/2pv^2 + pgh)Q = power) I get a slightly higher value for the power than the solution shows, however if I neglect the kinetic and potential energy terms I get the same answer as this solution. Should I ignore the kinetic and potential energy terms (1/2pv21/2pv^2 and pghpgh) in the power equation? Obviously the fluid has some velocity, but if the velocity does not change (or perhaps because the velocity given is an average value) should I just omit it from the equation?

Thanks!

Hi ts,
Thank you for this question. The kinetic energy and potential energy terms are relevant only if they are changing along the tube. The height of the two ends of the artery are presumed to be the same, and the speed of the blood is also assumed to be constant. The only thing changing along the length of the artery is the pressure, so only this term is non-zero in the expression you gave. Example 12.6 is similar to part (b) of this problem, and is good inspiration.
Also, notice that QΔP=vAΔP=vFQ\Delta P = vA \Delta P = v F, showing your suggested expression QΔPQ\Delta P is the same as the vFv F shown in the solution video.
All the best with your studies,
Shaun