Question
Prove that the speed of an incompressible fluid through a constriction, such as in a Venturi tube, increases by a factor equal to the square of the factor by which the diameter decreases. (The converse applies for flow out of a constriction into a larger-diameter region.)
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 12, Problem 14 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
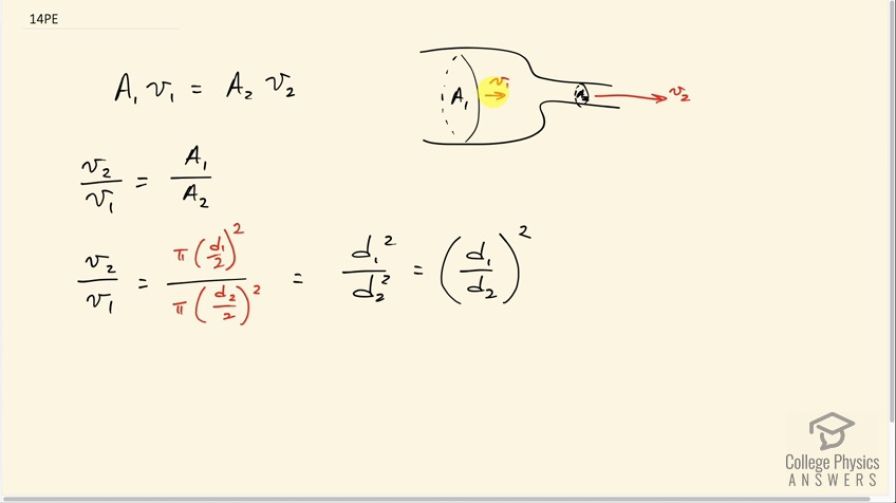
This is College Physics Answers with Shaun Dychko. A fluid is travelling through a tube of diameter one with area one and has some speed V one and it's going to go through a constriction of a smaller cross-sectional area tube A two and it's going to have a compensating the greater speed V two such that the volume rate of flow through this constricted portion will be the same as here. And that is the equation of continuity. And it says that, you know, if a certain volume of fluid has to pass through here, then that same volume will have to pass through here in the same amount of time. And in other words, the rate of volume flow has to be the same. Otherwise, there is either fluid either disappearing or being created, which of course, isn't gonna happen, or the fluid is being compressed. But we're told that the fluid in this case is incompressible. So that means area one times the speed of fluid through there at Section V one is going to equal area two multiplied by the speed of the fluid through that section V two. And we want to show that the speed V two is greater than V one by a factor equal to the square of the factor by which the diameters of these sections of pipe differ. So let's figure out what the ratio of V two over V one is, because the nettled, that it will be the factor by which they different and so divide both sides by A two and also divide both sides by V one and we get that V two over V one is A one over A two, so area one is PI times the radius squared, which is diameter one over two squared and area two is going to be pi times diameter two over two squared. And these PIs cancel and these denominator, you know… four of these squared cancels and we have d one squared over d two squared, this can be written as d one over d two all squared. And this is the factor by which the diameters are different. And so you'd also maybe read it a step further and say that V two is V one multiplied by a factor by which the diameter is a different squared. And there we go.