OpenStax College Physics, Chapter 12, Problem 43 (Problems & Exercises)

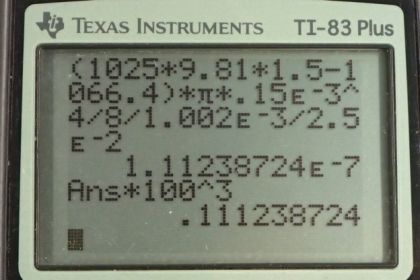
This is College Physics Answers with Shaun Dychko. The intravenous system for this patient has a hose with a radius of 0.15 millimeters, which is 0.15 times ten to the minus three meters, and the hose length is two and a half centimeters. The blood pressure at the needle is eight millimeters of mercury which we convert into pascals. The viscosity of the stuff in the IV tube, is the viscosity of water which is 1.002 times ten to the minus three pascal seconds. So the pressure due to the height of the fluid when it's 1.61 meters above the needle is the density of the solution inside, it's a saline solution so its density is 1025 kilograms per cubic meter, times 9.81 newtons per kilogram times the height between the pouch and the needle in the person's arm. So that's 1.61 meters, in this case 1.62 times ten to four pascals. Part B asks for what the rate of the fluid flow will be with a height of 1.50 meters instead of the height given to us in the example. So, the fluid flow rate will be the difference in the pressures, this is the pressure due to the height of the fluid and this is going to be the blood pressure that's pushing back on the fluid at the needle. So we take that pressure difference, multiply by pi times the radius of the IV tube to the power four, divided by eight times the viscosity of the saline solution, times the length of the tube. So, we have rho g h two, this h two distinguishes it from h in part A. We now have 1.50 meter for the height now, minus pressure of the blood. I substituted the number one with a subscript b there to say that this is the blood pressure. Then we plug in numbers, so it's 1025 kilograms per cubic meter density, times 9.81 newtons per kilogram, times 1.5 meters, minus 1066.4 pascals which is eight millimeters of mercury converted into pascals, then times pi, times 0.15 times ten to the minus three meters radius of the tube to the power four, divided by eight times the viscosity of 1.002 times ten to the minus three pascals seconds, times two and a half times ten to the minus two meters length of the tube. This works out to 0.111 cubic centimeters per second after you convert this number which is in cubic meters per second by multiplying by 100 centimeters for every meter three times to get into units of cubic centimeters per second. Part C, the flow will reverse when the pressure due to the height of the column of the saline solution equals the blood pressure. So we have rho g h for reversal, subscript r to mean the height at which point the flow can reverse, equals blood pressure and we solve for h r by dividing both sides by rho g. So the height for reversal of the IV will be 1066.4 pascals, divided by 1025 kilograms per cubic meter times 9.81 newtons per kilogram which is 0.106 meters which is 10.6 centimeters. So that means if a patient were to stand up and the IV bag was less than 10.6 centimeters above their arm, then the IV drip wouldn't go into their arm anymore. So this is the post it's usually on, some wheels here, and here's the bag with the saline solution in it and the hose connected to the needle in their arm. If this distance here is ever less than 10.6 centimeters, like if they lift their arm up to their head say, then the IV drip won't work anymore.