Question
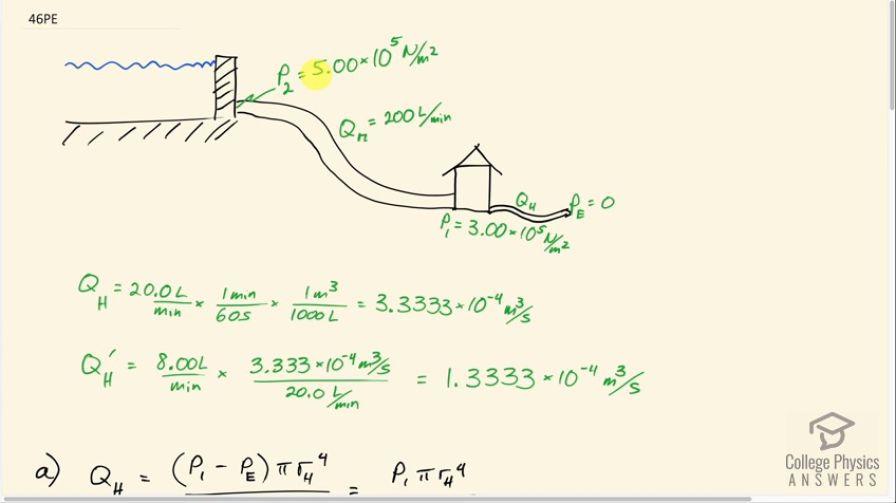
Water supplied to a house by a water main has a pressure of early on a summer day when neighborhood use is low. This pressure produces a flow of 20.0 L/min through a garden hose. Later in the day, pressure at the exit of the water main and entrance to the house drops, and a flow of only 8.00 L/min is obtained through the same hose. (a) What pressure is now being supplied to the house, assuming resistance is constant? (b) By what factor did the flow rate in the water main increase in order to cause this decrease in delivered pressure? The pressure at the entrance
of the water main is , and the original flow rate was 200 L/min. (c) How many more users are there, assuming each would consume 20.0 L/min in the morning?
Final Answer
- The water main flow rate increased by a factor of 1.90.
- 38 more people used water in the afternoon.
Solution video
OpenStax College Physics, Chapter 12, Problem 46 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a scenario where this water main is connected to some reservoir here and has a pressure of five times 10 to the five newtons per square meter here. We'll call that P two. The main has some flow rate in it of 200 liters per minute. And this is all at the beginning in the morning. I'm going to label things in the afternoon with a prime symbol on it. And we have this pressure at the house three times 10 to the five newtons per square meter. And this pressure at the end of the hose is zero. Now, of course, the pressure at the end of the hose is atmospheric pressure. But all these pressures, we presume to be gauge pressures. These are the amount by which the pressure exceeds atmospheric pressure. So the pressure in the hose, we might want to convert it into cubic meters per second. And so we multiply by one minute for every 60 seconds and then by every one cubic meter for every 1000 liters. But it turns out that we don't use any formulas that require the cubic meters per second formula or units. So we're gonna be using 20 liters per minute and eight liters per minute. But it was a good habit usually to convert units at this stage where we are writing things that we know, down. Part ‘A’ asks, what pressure is now being supplied to the house in the afternoon. So in the afternoon the flow rate through the hose is only eight liters per minute, whereas in the morning the flow rate to the hose, it's ‘H’ for hose is, was 20 liters per minute. So Perseus law for volume flow rate is that it's going to be the difference in pressure between the ends of the tube. And so we have the beginning of the hose is here with this pressure three times 10 to the five newtons per square meter in the morning, minus the pressure at the end, which is zero times pi times the radius of the hose to the fourth power divided by eight times the viscosity of the fluid, which in this case is water times the length of the hose. And then we’ve rewritten it just without the P E since the end pressure is zero. And the volume flow rate in the afternoon, which is what the prime symbol denotes, is the pressure at the beginning of the hose in the afternoon, P one prime. And that's what we're trying to find in this question part ‘A’ is P one prime minus zero, of course, at the end of the hose times pi times, all these other things. And we have the same expression as before but with a P one prime instead of a P one. So we can find the factor by which the flow rate changes. We know what that is because we can just divide these flow rates, eight liters per minute divided by 20 liters per minute and then that's going to be the same as dividing these expressions here. So we have Q H Prime is this one. And I've copied it here. And then dividing a fraction by a fraction is confusing. So instead I'm going to multiply by the reciprocal of the denominator fraction. So this is the fraction in the denominator here. So I'm going to multiply by it's reciprocal. So flipping it over and writing, multiply by eight new l h over P one pi R H to the fourth. And the common factors all cancel. And we're left with P one prime over P one, which means if you multiply both sides by P one, we have solved for P one prime. So P one prime is P one times the volume flow rate in the afternoon, divided by the volume flow rate in the morning. So the morning pressure is three times 10 to the five newtons per square meter, times eight liters per minute in the afternoon flow rate divided by 20 liters per minute, morning flow rate. And that is 1.20 times 10 to the five newtons per square meter. And that's a gauge pressure. This is the pressure in the afternoon. We expected this number to be lower than three times ten to the five, because the volume flow rate is lower, eight instead of 20. And that would be accounted for by everything else in the hose is the same, same radius, viscosity and length and so on. The only thing that's changed is the pressure at the beginning of the hose and so and so we expected this pressure to be lower. Good. Now, part ‘B’ by what factor did the flow rate in the water main increase in order to cause this decrease in delivered pressure at the house. So this Q M it was 200 liters per minute in the morning, but in the afternoon it's going to be higher than 200 liters per minute because so many more houses are using water. And the question is by what factor has it changed? So the volume flow rate it in the main, So ‘M’ denotes the water main in the morning is P two which is going to be the same in the morning and in the afternoon. There's no prime on P two here because it's controlled by this reservoir, which is at the same height in the morning or the afternoon. So the pressure is going to be the same. Or if it's not a reservoir, some pump that's gonna be operating the same. And so we have in the morning the Q M is P two minus P one times pi times the radius of the main to the fourth divided by eight times viscosity of water times, length of the main. And then in the afternoon it's gonna be everything the same except the P one prime, this pressure delivered to the house, which is the pressure at the beginning of the garden hose, will be different. So Q M prime divided by Q M is going to answer this question and that'll be the factor by which the volume flow rate in the water main increases in the afternoon. There's going to be this expression for Q M prime divided by this expression. But I'm writing that as multiply by it's reciprocal. So I flip this over and multiply here. And again, we have a whole bunch of common factors cancelling everywhere here and we have Q M prime over Q M then is P two minus P one prime divided by P two minus P one. So this is the reservoir beginning of the water main pressure, the same in the morning and afternoon. And this is the pressure delivered to the house in the afternoon. And this is the pressure delivered to the house in the morning. So this is Q M prime over Q M equals five times 10 to the five newtons per square meter, which we're told is P two minus the pressure supplied to the house in the afternoon, which we calculated in, in part ‘A’ here. So minus 1.2 times 10 to the five newtons per square meter divided by the water main beginning pressure minus the pressure delivered to the house in the morning, three times 10 to the five newtons per square meter. And this is 1.90. So, the water main flow rate increased by a factor of 1.90. Part ‘C’ says, how many more people are using water in the afternoon compared to in the morning? So the number of people will be the total flow rate in the water main, divided by the rate of water use per person in their garden hoses. So we're told that each person uses about 20 liters per minute in the morning. So that's 200 liters per minute, water main flow rate divided by 20 liters per minute per person in the morning. And that's 10 people in the morning. Then in the afternoon, which is what the prime means. We have this new water main volume flow rate, which is 1.9 times the morning volume flow rate. And we get that 1.9 from Part ‘B’ here, divided by the flow rate through the hose in the afternoon, which we're told is eight liters per minute. So that's 1.9 times 200 liters per minute. That's the volume flow rate in the afternoon in total and divide by eight liters per minute. That is 47.5 people are using water in the afternoon, of course, that's an estimate. That's why there's a 0.5 there. So let's take this to be 48 people in the afternoon, minus 10 people in the morning means there are 38 more people using water in the afternoon.

