Question
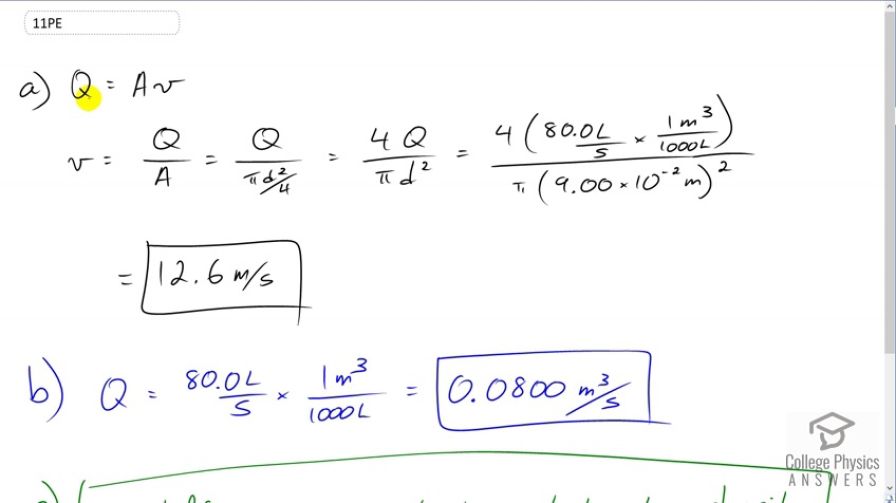
(a) What is the fluid speed in a fire hose with a 9.00-cm diameter carrying 80.0 L of water per second? (b) What is the flow rate in cubic meters per second? (c) Would your answers be different if salt water replaced the fresh water in the fire hose?
Final Answer
- No difference since flow rate does not depend on fluid density.
Solution video
OpenStax College Physics, Chapter 12, Problem 11 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to calculate the speed of the water going through this fire hose. And we're going to take the volume flow rate Q equal to the cross sectional area of the hose times the speed and we'll divide both sides by A and we solve for V. So V is the volume flow rate divided by the cross-sectional area. The cross-sectional area is Pi times the diameter of the hose square root over four. So this makes four Q over Pi d squared. So we have to convert units in order to be consistent on top and bottom and we're going to choose to have meters on the top and bottom. So we have four times 80 Liters per second multiplied by one cubic meter for every one thousand Liters so that we have cubic meters on top. And we divide that by Pi times 9.00 centimeters written as meters so centi is prefix meaning ten times minus two and we square that diameter. And we end up with 12.6 meters per second is the speed of the water. And in part b, what is the flow rate in cubic meters per second. Well, we take this 80 Liters per second and multiply it by one cubic meter for every thousand Liters and we end up with 0.0800 cubic meters per second. And if the hose were shooting salt water instead of fresh water will make no difference because this flow rate does not depend on density. And density difference is the only real difference between the salt and fresh water in this context.

