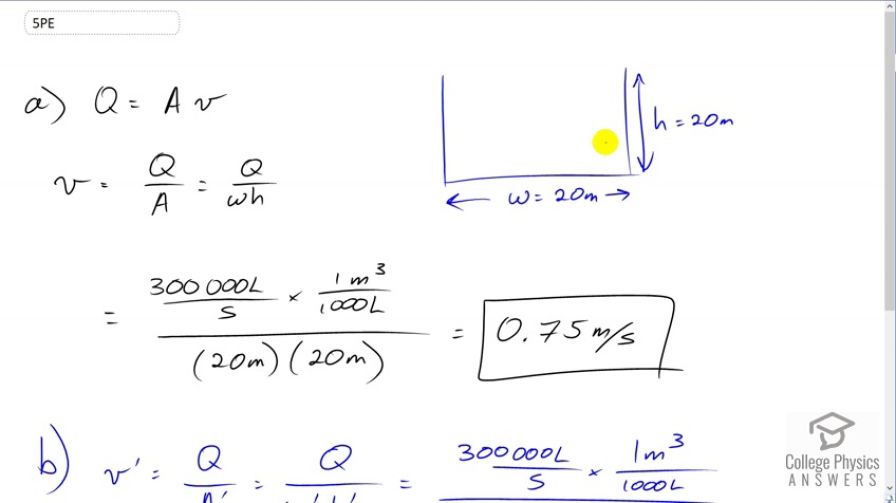
Question
The Huka Falls on the Waikato River is one of New Zealand's most visited natural tourist attractions (see Figure 12.29). On average the river has a flow rate of about 300,000 L/s. At the gorge, the river narrows to 20 m wide and averages 20 m deep. (a) What is the average speed of the river in the gorge? (b) What is the average speed of the water in the river downstream of the falls when it widens to 60 m and its depth increases to an average of 40 m?
Final Answer
Solution video
OpenStax College Physics, Chapter 12, Problem 5 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. At the gorge where the Waikato River of New Zealand narrows to a width of 20 meters and a height of 20 meters, we’re going to figure out what its speed is. And so the volume flow rate is equal to the cross sectional area of the river multiply by its speed. And we’ll solve for v by dividing both sides by A, and so v is Q over A. And the area is going to be the width times the height, so I have w times h at the denominator there. So the volume flow rate is 300000 liters per second, and we’re going to convert that into cubic meters per second, so that we can divide by the meters squared at the bottom. So we multiply by one cubic meters for every 1000 liters, and then divide by 20 meters width times 20 meters height, and we get 0.75 meters per second is the speed. And then when the river expands to a 60 meters width by a 40 meters height, we have the same numerator, and dividing it by 60 times 40, and this gives 0.13 meters per second when the river is wider, so it slows down when it’s wider and deeper.
