OpenStax College Physics, Chapter 29, Problem 84 (Problems & Exercises)

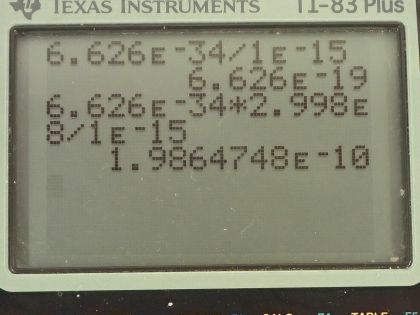
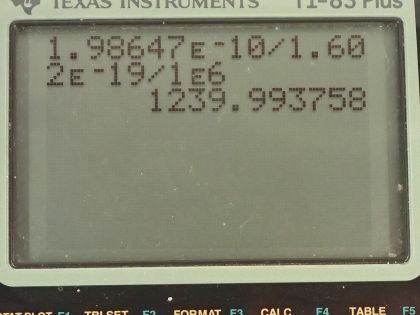
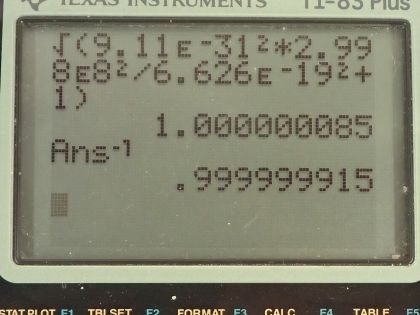
This is College Physics Answers with Shaun Dychko. A photon has a wavelength of 1.00 femtometer, which is 1.00 times 10 to the minus 15 meters and question (a) is what is the photon momentum? Well, the momentum is Planck's constant divided by the wavelength so that's 6.626 times 10 to the minus 34 joule seconds divided by 1.00 times 10 to the minus 15 meters and that's 6.63 times 10 to the minus 19 kilogram meters per second. And what is its energy in joules and megaelectron volts? Well the energy of a photon is Planck's constant times its frequency and we can use the wave equation, which says the speed of the wave is its wavelength multiplied by frequency because we want to substitute for f in terms of the wavelength that we are given. So we'll divide both sides of this by λ and so f equals c over λ and we substitute that in for f here and so the energy of a photon is 6.626 times 10 to the minus 34 joule seconds times speed of light divided by 1.00 femtometer and this works out to this many joules which we then convert into electron volts and then convert those electron volts into megaelectron volts by multiplying by 1 megaelectron volt for every 10 to the 6 electron volts and we end up with 1240 megaelectron volts or 1.99 times 10 to the minus 10 joules. Part (c) asks what is the relativistic velocity of an electron that has that same momentum that we calculated in part (a)? So momentum is this Lorentz factor multiplied by mass times velocity and Lorentz factor is 1 over square root 1 minus v squared over c squared and when we substitute that in, we have this expression for momentum: mass of the electron times its velocity divided by square root of 1 minus its velocity squared divided by speed of light squared. We can multiply both sides by square root 1 minus v squared over c squared and on the left, we get p times square root 1 minus v squared over c squared and on the right, we have mv then we can square both sides and we get p squared times 1 minus v squared over c squared equals m squaredv squared and then multiply p squared into the brackets and we get this line here and then we want to collect the terms that have the factor v in them together so we'll add v squaredp squared over c squared to both sides and then switch the sides around and we get m squaredv squared plus v squaredp squared over c squared equals p squared. and factor out the v squared and we get this line and then divide both sides by this bracket m squared plus p squared over c squared and you get this line here v squared equals p squared over m squared plus p squared over c squared and you could substitute in numbers at this point and actually when I first did this question, I did that but it turns out that with the types of numbers involved, your answer will be so close to the speed of light, you won't be able to tell really the difference between the speed of this electron and the speed of light to the precision that your calculator has. So I am going to instead rewrite this fraction in a different way so that we can express our answer as some number times c and then we'll be able to see that it's not exactly c, it's some number times c and this number is something that we'll be able to represent in our calculator. Okay! So what's going to happen here is we will multiply top and bottom by 1 over p squared so multiplying by 1 you could say of course and multiplying top and bottom by the same thing and that makes 1 on the top and divide it by m squared over p squared and then plus 1 over c squared and then at this point, we'll multiply top and bottom by c squared and you end up with c squared on the top and on the bottom, m squaredc squared over p squared plus 1 and then take the square root of both sides and v is now c divided by square root m squaredc squared over p squared plus 1 and so now this 1 over this square root is going to be that factor we were looking for multiplied by c. So we have c divided by square root of the mass of an electron squared times the speed of light squared divided by the momentum from part (a) squared plus 1 and this works out to c over 1 plus 8.5 times 10 to the minus 8; I wrote it this way just because it's too much writing to write so many decimals to have 1.0000 and so on till you get to 85 but then I did 1 over 1 plus 8.5 times 10 to the minus 8 and end up with this factor here which I wrote out in full. So the answer is 0.999999915c. Okay! Part (d) is asking for the electron's kinetic energy. So kinetic energy is γ minus 1 times mc squared— and this is the relativistic version for kinetic energy— and γ is 1 over square root 1 minus v squared over c squared so we substitute that in for γ here and so we have 1 over the square root of 1 minus the answer for part (c)— 0.999999915c— squared over c squared minus 1 times the mass of an electron times speed of light squared and this is 1.99 times 10 to the minus 10 joules.