Question
(a) If the position of an electron in a membrane is measured to an accuracy of , what is the electron’s minimum uncertainty in velocity? (b) If the electron has this velocity, what is its kinetic energy in eV? (c) What are the implications of this energy, comparing it to typical molecular binding energies?
Final Answer
- Table 29.1 shows this energy is nine orders of magnitude less than a weakly bound molecule. The electron would therefore not cause any molecules to break apart or atoms to ionize.
Solution video
OpenStax College Physics, Chapter 29, Problem 62 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
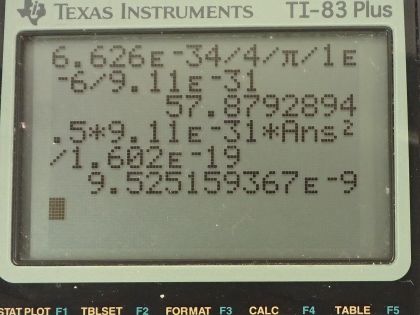
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The uncertainty in the position of an electron is 1.00 micrometer and the question is what must the uncertainty then be in the electron's velocity? The Heiseneberg uncertainty principle says that the product of the uncertainty in the position and the uncertainty in the momentum has to be greater than or equal to Planck's constant over 4π. We can replace uncertainty in momentum with uncertainty in mass times velocity and we'll assume that the uncertainty in the mass is really negligibly small in which case the total uncertainty in the momentum just comes from the uncertainty in the velocity so we will put this Δ symbol, this "change in", just on the v. So we can divide both sides by Δx times m and that gives us an expression for the uncertainty in the velocity. At its minimum, it's going to be Planck's constant over 4π times the uncertainty in position times mass. There's Planck's constant in joule seconds divided by 4π times the uncertainty in the position— 1.00 times 10 to the minus 6 meters— multiplied by the mass of an electron and this works out to 57.9 meters per second— that's the minimum uncertainty in the velocity. Part (b) says suppose the electron has this particular velocity what must its kinetic energy be in electron volts? Kinetic energy is one-half mass times its velocity squared so that's one-half times mass of an electron times the velocity we calculated in part (a) squared and this will give us an answer in joules so we have to convert it into electron volts by multiplying by 1 electron volt for every 1.602 times 10 to the minus 19 joules, this works out to 9.53 times 10 to the minus 9 electron volts. Part (c) asks what are the implications of this energy and compare it to typical molecular binding energies. So we can look at table [29.1] and the binding energy of a weakly bound molecule is 1 electron volt and so this energy is 9 orders of magnitude less than that the word 'orders of magnitude' refers to how many times or what power of 10 should you multiply to get from one number to the other approximately so this is 9 times or 9 orders of magnitude less than a weakly bound molecule. So it would therefore not cause any atoms to ionize and it wouldn't break apart any molecules and there we go!