Question
(a) What is the separation between double slits that produces a second-order minimum at for 650-nm light? (b) What slit separation is needed to produce the same pattern for 1.00-keV protons.
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 81 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
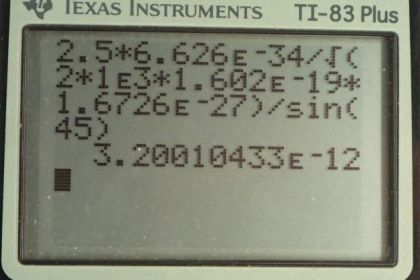
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In part (a) of this question, we need to figure out the separation between two slits such that 650 nanometer light will have a second order minimum at an angle of 45 degrees. And this is the formula from chapter 27, number 4 that tells us the relation between the separation between slits and the angle to the minima and the order and the wavelength. So we'll solve this for d by dividing both sides by sin Θ and we have the separation between slits is the order of the minimum plus a half times the wavelength of light divided by sin of the angle to the minimum. So we have 2 because this is a second order minimum plus a half times 650 times 10 to the minus 9 meters divided by sin 45 degrees giving us a separation between slits of 2.30 micrometers. In part (b), we are asked to figure out what slit separation is needed to produce the same pattern for 1 kiloelectron volt protons? So the same pattern meaning there's a second order minimum of 45 degrees, in other words. So the energy is 1 kiloelectron volt; that's the kinetic energy of the protons and we know that the wavelength of the protons because we need to have a a wavelength to substitute into this formula here. The de Broglie wavelength of the protons would be Planck's constant divided by momentum and momentum since we'll assume this is a non-relativistic speed to have this kinetic energy is going to be mv and we can substitute that in here which we'll do a little bit later. But before that let's figure out what this speed is based on kinetic energy because that's what we are given here and then we'll put this actually into there on this line here. OK. So we know momentum is this, we care about momentum because momentum is used to figure out the wavelength of the protons and then figure out the speed within this momentum formula we use kinetic energy which we are given which is one-half mv squared and we'll solve this for v by multiplying both sides by 2 over m and then take the square root of both sides. So the speed is square root 2 times kinetic energy over mass and we plug that into the momentum formula which we do here and m multiplied by square root 1 over m you can put the m inside the square root sign because you can think of this as square root of m squared bringing this m into the square root times 2KE over m and this m cancels with one of those m's leaving us with 2 times kinetic energy times mass. That gets plugged into the denominator of the de Broglie wavelength formula and we do that here. And all of this gets plugged into our formula for the separation between the slits. So now we are replacing lambda with h over square root 2 times kinetic energy times mass and we do that here. So the separation between slits is the order plus a half times Planck's constant over the square root of 2 times kinetic energy times mass times sin of the angle to the minimum. So we have a second order minimum so we replace the letter m with number 2 plus a half times Planck's constant divided by square root of 2 times the energy— 1 times 10 to the 3 electron volts—that's the kinetic energy times the we have to convert it into joules in order to have mks units because all the other factors in our formula have mks units and so we convert it into that by multiplying by 1.602 times 10 to the minus 19 joules per electron volt and then we multiply by the mass of the proton, square root all that and then multiply by sin 45 and we get 3.2 times 10 to the minus 12 meters should be the separation between the slits in order for a proton to have a second order minimum at 45 degrees.