Question
Sunlight above the Earth’s atmosphere has an intensity of . If this is reflected straight back from a mirror that has only a small recoil, the light’s momentum is exactly reversed, giving the mirror twice the incident momentum. (a) Calculate the force per square meter of mirror. (b) Very low mass mirrors can be constructed in the near weightlessness of space, and attached to a spaceship to sail it. Once done, the average mass per square meter of the spaceship is 0.100 kg. Find the acceleration of the spaceship if all other forces are balanced. (c) How fast is it moving 24 hours later?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 86 (Problems & Exercises)
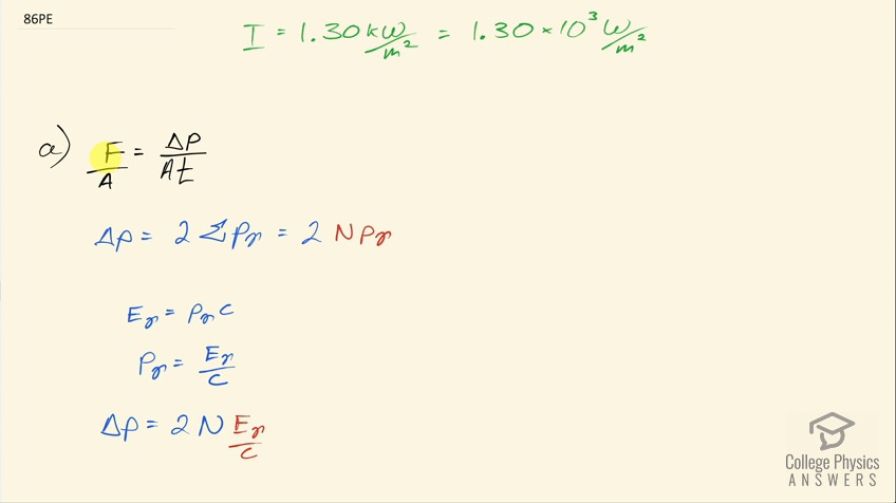
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
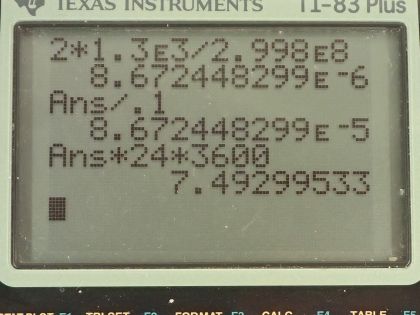
This is College Physics Answers with Shaun Dychko. Above the Earth's atmosphere, sunlight has an intensity of 1.30 kilowatts per square meter and in question (a), we are asked if this sunlight hits a mirror in space what is going to be the force per area on the mirror knowing that the change in momentum of a photon that reflects off the mirror will be 2 times the original momentum that the photon has? So if the mirror is here and the photon has some momentum going to the right say— this is p initial— and then the momentum final after reflection will be negative of that— same momentum— and so the change in momentum— p final minus p initial— is going to be negative p γ minus p γ which is negative 2p γ— the negative sign's not important here; the important part is just to know that the magnitude of this change of momentum is 2 times the initial momentum of the photon. Okay! So that's to say that Δp— this change in momentum— is going to be 2 times the total momenta of all the incident photons. So here we have force per area is the rate of change of momentum divided by momentum where I have F equals Δp over t— this is Newton's Second Law the original way that he wrote it instead of writing F equals ma, he wrote the rate of change of momentum— and then just dividing both sides by area because the question is asking us for force per area. Okay! So we are going to replace Δp— this change in momentum— with 2 times the momentum of every photon and so that is the number of photons multiplied by the momentum of a single photon. Now to find the momentum of a single photon, we use this equation which says that the energy of the photon equals its momentum multiplied by speed of light and we can divide both sides by c to get that the momentum of a single photon is its energy divided by speed of light and then substitute this in place of p γ for our change in momentum and so our total change in momentum then after all the photons strike the mirror is 2 times the number of photons times the energy of a single photon divided by speed of light. So this gets substituted in for Δp and we do that here and so the force per area then is 2 times the number of photons times the energy of a single photon divided by the area multiplied by time times the speed of light. Now all this stuff here— NE γ over At— this is intensity so this numerator is the total energy because this is the number of photons multiplied by the energy for a single photon and then we are dividing that by time, which is power and then we are dividing that power by area, which is intensity so we can replace NE γ over At all with I so the force per area then is 2 times intensity over speed of light. So that's 2 times 1.30 times 10 to the 3 watts per square meter divided by 2.998 times 10 to the 8 meters per second and that's 8.67 times 10 to the minus 6 newtons per square meter. In part (b), we are told that the mirror is attached to a spaceship and the combined mass per area of the mirror and spaceship together is 0.100 kilograms per square meter in that case, what will the acceleration of the spaceship be? So force is mass times acceleration and we don't know the force though we just know the force per area— that's what we calculated in part (a)— so we can divide both sides by area here and so we have force per area equals mass per area times acceleration and we can solve this for acceleration by dividing both sides by the mass per area so acceleration then is force per area divided by mass per area. So that's 8.67245 times 10 to the minus 6 newtons per square meter divided by 0.100 kilograms per square meter and that's 8.67 times 10 to the minus 5 meters per second squared. So that's a very small acceleration but given enough time, it will achieve high velocities; after 24 hours, we see that that acceleration multiplied by 24 hours converted into seconds is going to be 7.49 meters per second and every day the speed will increase by this much.