Question
(a) Calculate the momentum of a photon having a wavelength of . (b) Find the velocity of an electron having the same momentum. (c) What is the kinetic energy of the electron, and how does it compare with that of the photon?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 42 (Problems & Exercises)
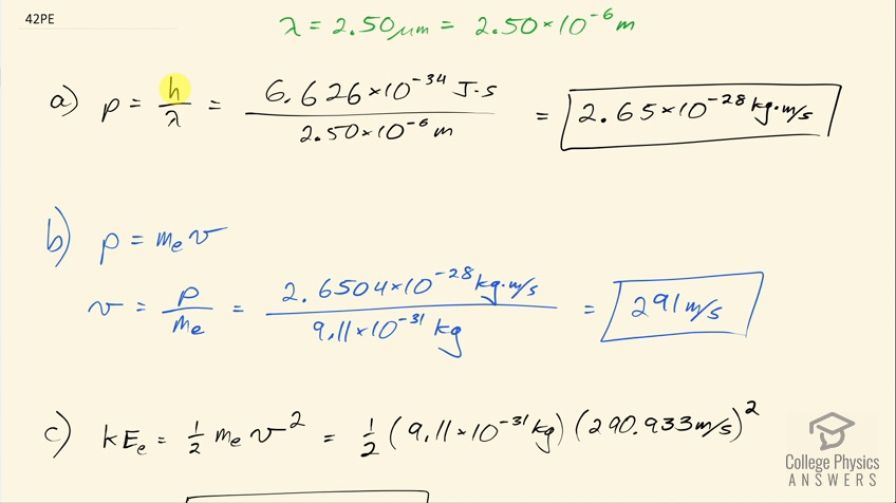
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the momentum of a photon that has a wavelength of 2.50 micrometers the formula is Planck's constant divided by the wavelength so that's 6.626 times 10 to the minus 34 joule seconds divided by the wavelength and that's 2.65 times 10 to the minus 28 kilogram meters per second. In part (b), we want to find the velocity of an electron that would have the same momentum so we have the same momentum then as the mass of an electron times its velocity and we will divide both sides by the mass of an electron to solve for v. So the velocity then is the momentum divided by 9.11 times 10 to the minus 31 kilograms— mass of an electron— and that's 291 meters per second. Part (c) asks what is the kinetic energy of this electron? Well that will be one-half times its mass times its velocity squared and here we have one-half times 9.11 times 10 to the minus 31 kilograms times its velocity we calculated in part (b) squared and that's 3.85 times 10 to the minus 26 joules and we are meant to compare this to the energy of the photon and the energy of a photon is its momentum times the speed of light and that works out to 7.95 times 10 to the minus 20 joules and to compare these numbers, we'll divide them so we'll take the energy of the photon and divide that by the kinetic energy of the electron and this works out to 2.06 times 10 to the 6, which means the photon energy is 2.06 times 10 to the 6 times larger than the kinetic energy of the electron and we expected the photon energy to be much larger because since mass and energy are equivalent a lot of the mass energy of the electron is contained within its mass and so that leaves not much leftover for its kinetic energy and there we go!


