Question
(a) Calculate the velocity of an electron that has a wavelength of . (b) Through what voltage must the electron be accelerated to have this velocity?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 58 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
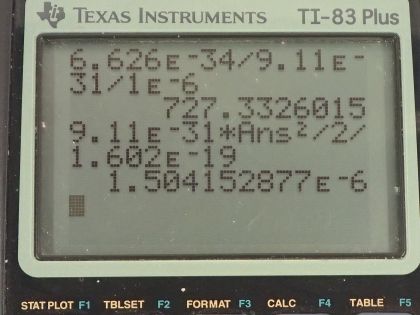
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are told that an electron has a de Broglie wavelength of 1.00 micrometer, which is 1.00 times 10 to the minus 6 meters and the question is what speed must it be going? Well the wavelength is Planck's constant divided by the momentum of the electron and we are told that... or we assume anyhow that the speed is non-relativistic in which case we are going to substitute the formula mass times velocity in place of momentum. If it was relativistic speeds by the way, we would have to have a γ here at this Lorentz factor for the momentum. Okay! We are going to solve this for v by multiplying both sides by v over λ and multiply this side by v over λ and we have v on the left then is Planck's constant divided by mass times wavelength on the right. That's 6.626 times 10 to the minus 34 joule seconds divided by the mass of an electron multiplied by its wavelength of 1.00 micrometer written as 1.00 times 10 to the minus 6 meters and that's 727 meters per second. Part (b) says through what voltage must the electron be accelerated to have this velocity? And we'll assume that the electron starts at rest and then it gets accelerated through a potential V and the potential energy that it will lose when it's accelerated through this potential would be the charge multiplied by that potential and that potential energy lost will equal the kinetic energy that it gains and we know the speed here and we know the mass and we know the charge and so we'll solve this for V—the voltage. So we divide both sides by q and we get the voltage then is mass times velocity squared over 2 times the charge... that's 9.11 times 10 to the minus 31 kilograms— mass of an electron— times the speed we calculated in part (a) squared divided by 2 times the elementary charge on an electron— 1.602 times 10 to the minus 19 coulombs— and this works out to 1.50 microvolts.