Question
Suppose the velocity of an electron in an atom is known to an accuracy of (reasonably accurate compared with orbital velocities). What is the electron’s minimum uncertainty in position, and how does this compare with the approximate 0.1-nm size of the atom?
Final Answer
is larger than the size of the atom by a factor of .
Solution video
OpenStax College Physics, Chapter 29, Problem 64 (Problems & Exercises)
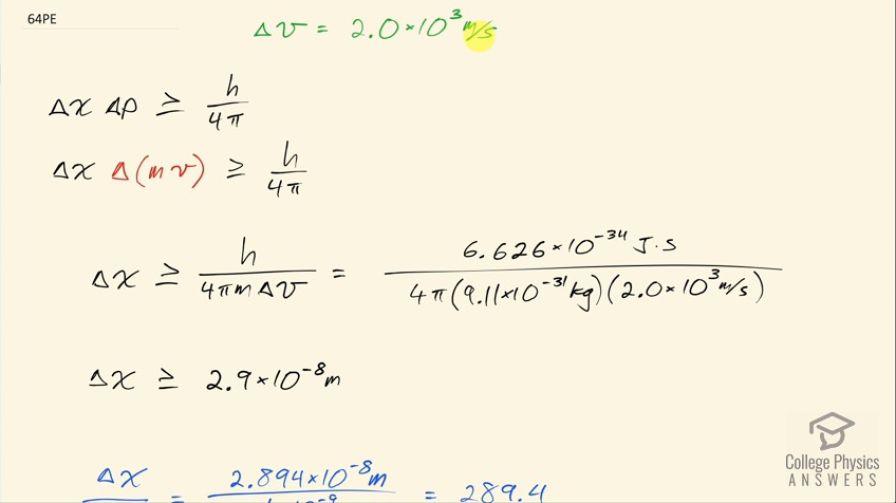
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The uncertainty in the velocity of an electron orbiting an atom is 2.0 times 10 to the 3 meters per second and the question is what is the minimum uncertainty in the position then of the electron given this uncertainty in its velocity? So the uncertainty in position times the uncertainty in momentum is more than or equal to Planck's constant over 4π and we can substitute mv in place of p and we know this is a non-relativistic situation because this speed is much less than the speed of light and we can solve this for Δx by dividing both sides by Δmv and we'll assume the uncertainty in mass is really small in which case this Δ applies just to the velocity so the uncertainty in momentum is going to be attributable entirely to the uncertainty in the velocity so we divide by mass times Δv. So the uncertainty in position then is more than or equal to Planck's constant over 4π times mass times uncertainty in velocity that's 6.626 times 10 to the minus 34 joule seconds divided by 4π times the mass of an electron times the uncertainty in velocity of 2.0 times 10 to the 3 meters per second and that means the uncertainty in position is more than or equal to 2.9 times 10 to the minus 8 meters. We are asked to compare this uncertainty in position with the size of the atom, which I take to mean the diameter of the atom so we'll take this uncertainty in position and divide it by the diameter of an atom so we have that divided by 0.1 times 10 to the minus 9 meters— we are told an atom is about 0.1 nanometers and so that's written as 0.1 times 10 to the minus 9 meters— and this is 290 or so. So the uncertainty in position is larger than the size of the atom by a factor of about 290.