Question
The decay energy of a short-lived particle has an uncertainty of 1.0 MeV due to its short lifetime. What is the smallest lifetime it can have?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 68 (Problems & Exercises)
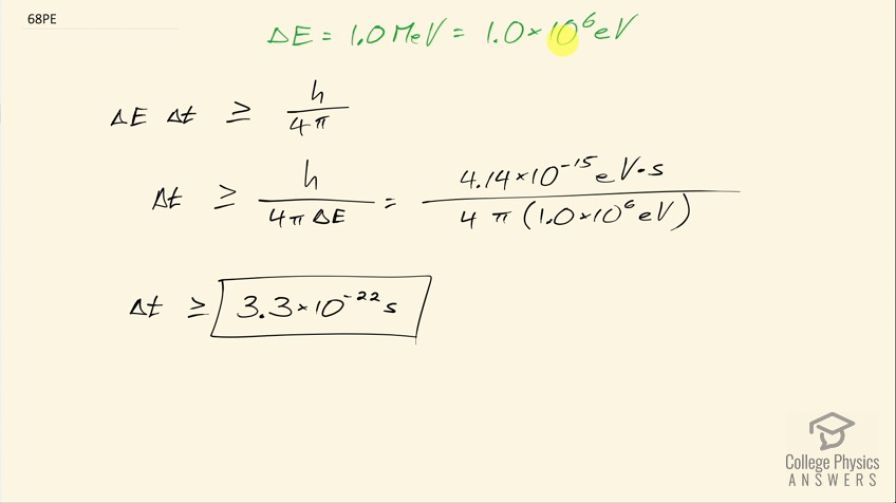
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The uncertainty in the amount of energy released by the decay of a short-lived particle is 1.0 megaelectron volt so that's 1.0 times 10 to the 6 electron volts and the question is what is the uncertainty then in the lifetime of the particle? So we know uncertainty in energy times uncertainty in lifetime is greater than or equal to Planck's constant over 4π and so we can divide both sides by uncertainty in energy to solve for the uncertainty in the lifetime and that's going to be Planck's constant divided by 4π times the uncertainty in energy. We are choosing this value for Planck's constant because the electron volts in the units here will cancel with the electron volts given to us by the question so it's convenient; I could have done 6.626 times 10 to the minus 34 joule seconds but then we would have to convert that number in order to well... we would have to convert to make the units work together so we would have to take the denominator and turn it into joules I suppose. So we have 4.14 times 10 to minus 15 electron volt seconds divided by 4π times 1.0 times 10 to the 6 electron volts. So the minimum uncertainty in the lifetime then is 3.3 times 10 to the minus 22 seconds.
