Question
(a) What is for a proton having an energy of 1.00 TeV, produced by the Fermilab accelerator? (b) Find its momentum. (c) What is the proton’s wavelength?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 78 (Problems & Exercises)
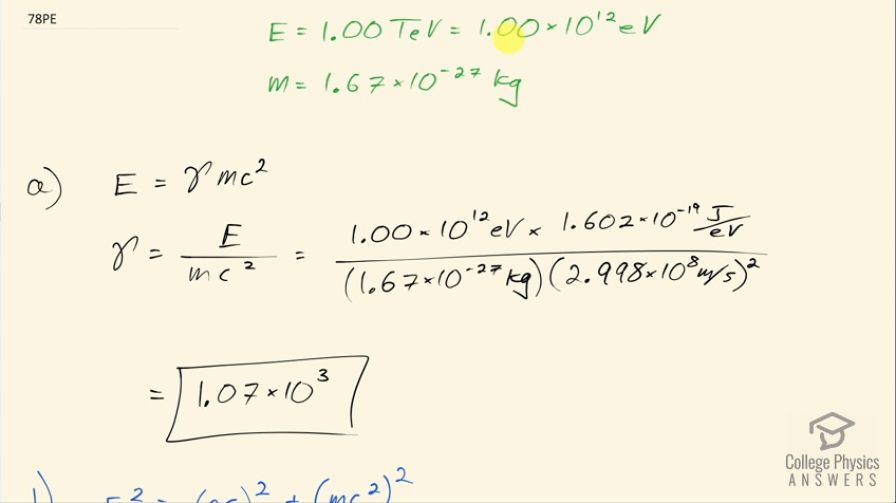
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
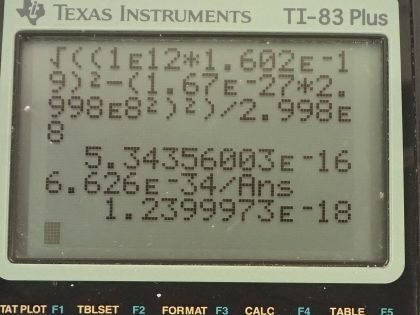
This is College Physics Answers with Shaun Dychko. A proton is accelerated in the Fermilab to an energy of 1.00 teraelectron volt— that is 1.00 times 10 to the 12 electron volts— the mass of a proton is 1.67 times 10 to the minus 27 kilograms; in part (a), we are asked to figure out what is γ, this Lorentz factor, and the total energy of the proton is γ times its mass times speed of light squared and we can solve for γ by dividing both sides by mc squared. So γ then is the energy divided by mass times speed of light squared. That's 1.00 times 10 to the 12 electron volts which we convert into joules by multiplying by 1.602 times 10 to the minus 19 joules for every electron volt and divide by the mass of a proton times the speed of light squared and that is 1.07 times 10 to the 3 is γ. Part (b) is asking for the momentum of the proton. We know that the relativistic equation for the total energy of the proton squared equals the momentum times speed of light all squared plus its rest energy all squared and we are going to solve this for p first by subtracting mc squared squared from both sides and then switch the sides around and we get pc squared equals E squared minus mc squared squared and then take the square root of both sides and you get this line here which we then divide both sides by c and we have momentum then is the square root of the total energy squared minus the rest energy squared all divided by speed of light. So that's the square root of 1.00 times 10 to the 12 electron volts converted into joules squared minus the mass of a proton times speed of light squared all squared all divided by the speed of light and this is 5.34 times 10 to the minus 16 kilogram meters per second. And then in part (c) we are asked what is the proton's wavelength? Its de Broglie wavelength is Planck's constant divided by its momentum. So that's 6.626 times 10 to the minus 34 joule seconds divided by this momentum that we found in part (b) and this works out to 1.24 times 10 to the minus 18 meters.