OpenStax College Physics, Chapter 29, Problem 82 (Problems & Exercises)

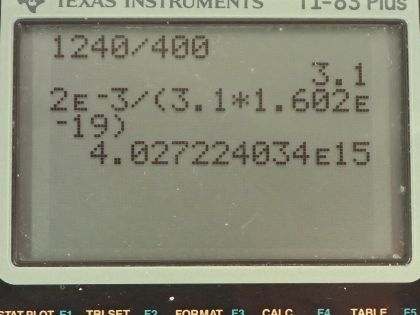
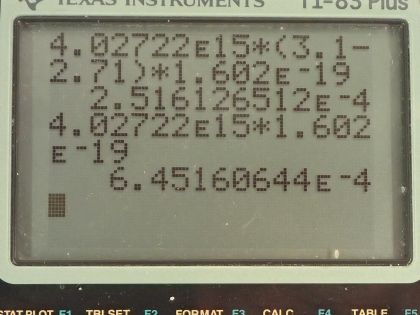
This is College Physics Answers with Shaun Dychko. A laser with a power output of 2.00 milliwatts is projected onto some calcium metal and the light has a wavelength of 400 nanometers and question (a) is asking how many electrons per second are ejected from the calcium metal? The first thing we need to know is does the energy of each photon exceed the binding energy of the material because it won't eject any electrons at all if the photon energy is below the binding energy and we are told in part (b) that the binding energy is 2.71 electron volts. So let's find the energy of the photons then. That's Planck's constant times the frequency and we'll use this wave equation to figure out what is the frequency in terms of the wavelength that we're given. So the speed of a wave equals the wavelength multiplied by frequency and we can divide both sides by λ to solve for f so frequency is c over λ and we'll plug that in for frequency and we'll do that here. So the energy for a single photon then 1240 electron volt nanometers choosing this convenient number for the product of Planck's constant and speed of light since the units of nanometers will cancel with the nanometers in our wavelength leaving us with electron volts in our answer so the energy of the photon then is 3.1 electron volts. So that 3.1 electron volts exceeds the binding energy of 2.71 electron volts and so every single photon can eject an electron. So that means the number of electrons ejected per second is the same as the number of photons produced by the laser per second. So the number of photons... or the power of the laser and this γ here just symbolizes I am talking about photons or light year; the power output of the laser is the number of photons produced multiplied by the energy per photon divided by time and it's this N over t that we want— this number per time... number of photons per second in other words. And so we'll divide both sides by the energy for a single photon and we get then that the rate of photon production then is the power of 2.00 times 10 to the minus 3 watts divided by 3.10 electron volts per photon times 1.602 times 10 to the minus 19 joules per electron volt because we need joules in the denominator here and then this works out to 4.03 times 10 to the 15 photons per second and so which is, you know, the number of electrons per second so really that's what they are asking for so let's write down electrons per second here. Okay! Good! Part (b) is what power is carried away by the electrons? And that will be in other words what kinetic energy is being carried away per time? So that will be the number of electrons multiplied by the kinetic energy of a single electron divided by time. The kinetic energy of the electron at its most is going to be the energy of the incoming photon minus the binding energy. Now we are taking the maximum kinetic energy of the photon here so this is the maximum possible power that could be taken away by the electrons. So we know what N over t is— the rate at which electrons are ejected and that's the answer for part (a)— and so we multiply that by the energy of a single photon minus the binding energy and then convert this difference, which has units of electron volts into joules and then this works out to 0.252 milliwatts. Part (c) is asking calculate the current of ejected electrons. So current is the amount of charge that passes a point per time and the amount of charge will be the number of electrons multiplied by the number of coulombs per electron or the elementary charge in other words. And this N over t is the answer for part (a) and then we multiply that by the elementary charge of 1.602 times 10 to the minus 19 coulombs per electron, the electrons cancel and we are left with coulombs per second and that is abbreviated amps so that's 6.45 times 10 to the minus 4 amps. Part (d) says imagine that the material is like a capacitor with a capacitance of 2.00 picofarads and the question is how long will current flow before the capacitor voltage stops the flow? So we imagine that the materials like this capacitor here where these are two parallel plates and this incident photon strike the material here, ejects an electron and that electron has some velocity or some kinetic energy and it will be able to travel to the other plate only if it has enough kinetic energy to overcome the voltage that is between the plates. So this plate will accumulate a negative charge over time as more electrons are deposited there to the point where there is a sufficient voltage such that the voltage is going to equal the kinetic energy of these electrons and that's the point where electrons won't make it anymore. So the current stops when the potential energy difference, which is the charge on a single charge multiplied by the potential difference in volts when that product equals this kinetic energy of an ejected electron at its most then that's when the current stops. So we need to substitute for voltage and we know that capacitance is the amount of charge built up on the plates divided by voltage and we can rearrange this for V by multiplying both sides by V over C and so V then is the amount of charge divided by capacitance and current is the amount of charge per time and we can rearrange this for Q by multiplying both sides by time and so this total charge then built up on the capacitor is the current multiplied by the amount of time and the current is the amount of charge on a single electron multiplied by the rate of electron production and this all gets substituted in for Q in our expression for voltage so we put that here and then all of this gets substituted in for voltage in this equation here. And so we have elementary charge squared times the rate of electron production multiplied by time divided by capacitance equals the kinetic energy of a single electron at its most and we can solve this for t by multiplying both sides by capacitance divided by charge squared times rate of electron production. So the time then is 2.00 times 10 to the minus 12 farads— 10 to the minus 12 is the prefix 'pico'— and we multiply that by the maximum energy of the ejected electron— kinetic energy that is— and that's 3.1 electron volts minus 2.71 electron volts so that's energy of the photon minus the binding energy converted into joules and then divide that by the elementary charge squared times the rate of electron production— answer for part (a)— and this works out to 1.21 nanoseconds.