Question
What is the maximum velocity of electrons ejected from a material by 80-nm photons, if they are bound to the material by 4.73 eV?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 14 (Problems & Exercises)
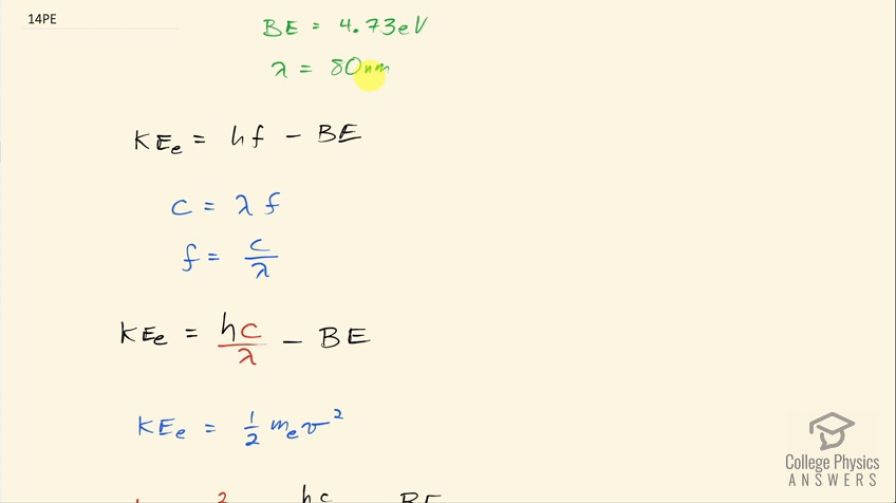
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
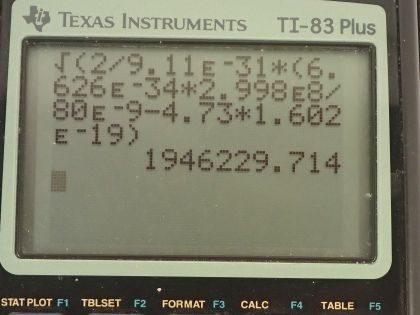
This is College Physics Answers with Shaun Dychko. We want to know the maximum velocity of electrons ejected from a material by 80 nanometer photons given a binding energy of 4.73 electron volts. Now we have an expression for kinetic energy of the electron so we'll figure that out first and then we will substitute one-half mass times velocity squared in place of kinetic energy and solve for v. Okay so kinetic energy is the total energy of the photon, which is Planck's constant times its frequency minus the binding energy but we are given the wavelength of the photon so we better substitute for f in terms of λ. The wave equation tells us that the speed of light equals the product of the wavelength and the frequency and we'll divide both sides by the wavelength to solve for frequency so frequency is speed of light divided by λ and we'll substitute that in for f, which we do here. Now we have another expression for kinetic energy of the electron which is one-half times the electron's mass times its velocity squared so we will substitute that in place of kinetic energy here and then multiply both sides by 2 over mass of the electron and then we get this expression, take the square root of both sides to solve for the velocity and so the speed of this electron then is the square root of 2 over the mass of the electron times Planck's constant times speed of light divided by the wavelength minus the binding energy. Now since we have a kilogram unit here that sort of informs what units we have to use for Planck's constant; often when I see hc together, I like to use 1240 electron volt nanometers that's often a good choice for convenience but in this case because we are mixing with kilograms, we need to use mks units—meters, kilograms and seconds. So we have 2 divided by 9.11 times 10 to the minus 31 kilograms— that's the mass of the electron times 6.626 times 10 to the minus 34 joules seconds— Planck's constant— times the speed of light divided by the wavelength in meters so that's 80 times 10 to the minus 9 meters minus 4.73 electron volts converted into joules because joules is an mks unit so we multiply by 1.602 times 10 to the minus 19 joules for every electron volt and this works out to 1.95 times 10 to the 6 meters per second.