OpenStax College Physics, Chapter 29, Problem 36 (Problems & Exercises)

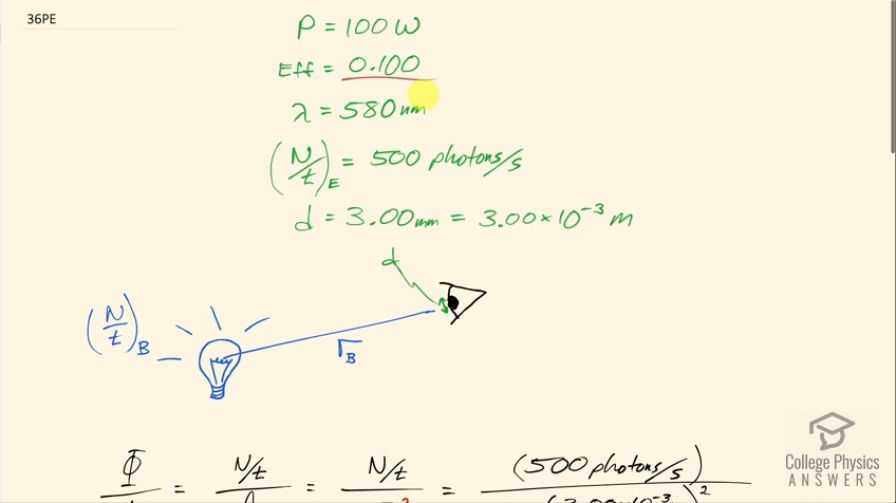
This is College Physics Answers with Shaun Dychko. This is a 100 watt light-bulb and 10 percent of the power output goes towards producing light with an average wavelength of 580 nanometers so the visible light power output is 10 percent of a 100 watts and the rate at which photons are entering the eye is going to be 500 photons per second we are told and this eye-pupil has a diameter of 3.00 millimeters. So this eye is some distance r B for 'bulb'— this distance away from the bulb— and we want to figure out what this distance should be such that the eye is receiving only 500 photons per second? So we need to find the rate of flux that will exist here at the pupil and so that's going to be the rate at which the photons are entering the eye— this is the number of photons per time divided by the area of the eye— so the eye pupil we will consider to be a circle and so its area is going to be π times its radius squared and this r has a subscript E for 'eye' and that's going to be half the diameter so I am plugging in half of 3.00 millimeters, written as 3.00 times 10 to the minus 3 meters. So we have 500 photons per second divided by π times this radius squared and this is 7.07355 times 10 to the 7 photons per second per meter squared so that's the rate of flux at the pupil. And we can also create an expression for the rate of flux at any distance from the bulb in terms of the rate of photon production by the bulb divided by the area over which those photons are spread. So we assume that the photons are being radiated evenly in all directions from the bulb and that the atmosphere is not going to be trapping any of the photons so it's not going to be blocking them. And so that means at a certain distance from the bulb, the photons will all be distributed over the area of a sphere at that distance and so the sphere we are interested in is this one with a radius r B at the distance of the pupil and the rate of flux at this position— we have just figured out—it should be this and so now the question is at what distance given the rate of photon production by the bulb will that rate of flux happen? So we have this rate of flux with no subscript on it there's no subscript B here even though everything here is in terms of the bulb because this rate of flux has to be the same as what we calculated for the eye and so this rate of flux here for the eye is equal and so since this and this are equal, we are not putting any subscripts on them but we are rewriting the expression for rate of flux now in terms of the bulb because now we have this factor r B here that we are going to solve for. So this is the rate of photon production by the bulb divided by the area of the sphere some distance r B from the bulb and so the formula for the area here is 4π times the distance from the bulb squared because this is the area of a sphere, not the area of a circle; over here we had the area of the pupil, which was a circle and down here we have the area of a sphere some distance away from the bulb. Okay! So what is this numerator then— the rate at which photons are produced— that's the next question here; this is going to be the power output, which is in joules per second which is another way of writing watts. So that joules per second is being divided by the energy per photon so when you have joules per second divided by joules per photon, this is the same as joules per second multiplied by the denominator flipped over which is photons per joule and the joules cancel leaving us with photons per second, which is why it is this... why it is going to be the number of photons per second from the bulb that we are looking for. So the power is going to be multiplied by the efficiency because 90 percent of the power goes into producing other things than visible photons and we just want the component for visible photons. So we multiply power by efficiency and divide by the energy per photon. The energy per photon is Planck's constant times speed of light divided by the wavelength of the photon and multiply top and bottom by λ to get this expression here. So the number of photons per second produced by the bulb is going to be 0.100—efficiency— times 100 watts times 580 times 10 to the minus 9 meters— average wavelength— divided by Planck's constant times the speed of light and that is 2.919745 times 10 to the 19 photons per second. So we can... we are going to rearrange this expression here and solve it for r B squared multiplying by r B squared and divide by this rate of flux and the r B squared cancels there and on this side, we'll have the same r B squared over rate of flux and so we have r B squared equals the rate of photon production by the bulb divided by 4π times the rate of flux and take the square root of both sides to solve for r B then. So the distance from the bulb is going to be the square root of the rate at which photons are produced by the bulb divided by 4π times the rate of flux. So that's 2.919745 times 10 to the 19 photons per second divided by 4π times 7.07355 times 10 to the 7 photons per meter squared per second and this is going to be 181 kilometers and that's the distance you will need to be from the bulb to perceive only 500 photons per second per square meter and this distance is much larger than you would expect based on experience and so in experience, I think what you would notice is that the atmosphere will be absorbing some photons; normally, you wouldn't experience being able to go 181 kilometers away from a 100 watt bulb and be able to see it. Okay!