OpenStax College Physics, Chapter 29, Problem 74 (Problems & Exercises)

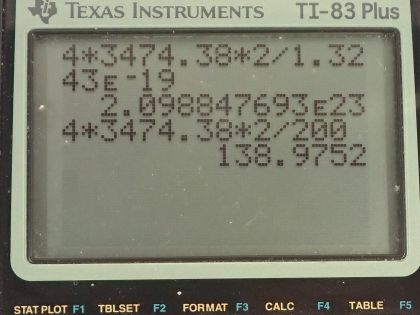
This is College Physics Answers with Shaun Dychko. A 200 watt heat lamp emits radiation with a wavelength on average of 1500 nanometers and question (a) asks what is the average photon energy in joules? So this is the energy for a single photon. That is Planck's constant times the photon frequency and we can figure out the frequency in terms of the wavelength by using the wave equation which says the speed of a wave is its wavelength multiplied by frequency and then we can divide both sides by λ to solve for f and so the frequency then is speed of light divided by the light's wavelength and we can substitute this in place of f here and so the energy of a single photon then is Planck's constant times speed of light divided by the wavelength. Now normally I would put in 1240 electron volt nanometers in place of h times c but in this case, it asks for the answer in units of joules and so we'll use the mks units for everything. So Planck's constant is 6.626 times 10 to the minus 34 joule seconds, we'll multiply that by the speed of light in meters per second and divide that by the wavelength in meters 1500 times 10 to the minus 9 meters and this is 1.32 times 10 to the minus 19 joules is the energy of a single photon. In part (b) it asks how many of these photons are needed to increase the temperature of a person's shoulder that has a mass of 4.0 kilograms by 2.0 Celsius degrees? I should also put in ΔT then is 2.0 Celsius degrees. The specific heat of the shoulder we are told is 0.83 kilocalories per kilogram per Celsius degree and I am going to convert this into mks units, in other words, we'll have joules in place of kilocalories here by multiplying by 4186 joules for every kilocalorie and so our specific heat then is 3474.38 joules per kilogram per Celsius degree. So the amount of heat from this infrared radiation is going to equal the mass of the shoulder times its specific heat times its change in temperature and this energy is coming from the photons and so we'll take the energy for a single photon and multiply that by the number of photons and so we substitute N times energy per photon in place of Q here so we have N times energy per photon equals mass of the shoulder times specific heat times change in temperature and then we'll solve this for N— the number of photons— by dividing both sides by the energy per photon. So the number of photons then is 4.0 kilograms times 3474.38 joules per kilogram per Celsius degree times 2.0 Celsius degrees divided by 1.3243 times 10 to the minus 19 joules per photon and this works out to 2.1 times 10 to the 23 photons. I have only two significant figures here because this mass has only two significant figures. In part (c), we are asked how long does this change in temperature take? So the power output of the lamp equals the total energy it has to deliver divided by the time it takes and we can solve this for t by multiplying both sides by t over power. So the time then is the energy delivered divided by the power and the energy delivered is the mass of the shoulder times its specific heat times the change in temperature divided by power. So that's 4.0 kilograms times specific heat times 2.0 Celsius degrees divided by 200 watts and this is 1.40 times 10 to the 2 seconds again with two significant figures since the shoulder mass has only two significant figures.