OpenStax College Physics, Chapter 29, Problem 32 (Problems & Exercises)

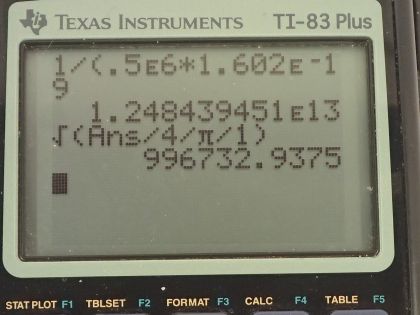
This is College Physics Answers with Shaun Dychko. The nuclear reactor in a satellite produces gamma rays with a power of 1.00 watt and the energy for each gamma ray photon is 0.500 megaelectron volts which is 0.500 times 10 to the 6 electron volts and the question is what is the rate of production of photons? So the power is the rate of production of photons multiplied by the energy per photon and so we can divide both sides by energy of a single photon and then we get the number of photons produced per time is power divided by energy per photon. So that's 1.00 joule per second that's what a watt is and I wrote it as joules per second just to see that in our final units here, we'll have per second since we have per second in these units for watts written as joules per second. So we have 1.00 joule per second divided by 0.500 times 10 to the 6 electron volts converted into joules in order to cancel with the joules in the numerator and that is multiplying by 1.602 times 10 to the minus 19 joules per electron volt and we end up with 1.25 times 10 to the 13 photons produced per second. Part (b) is saying how far away must another satellite be to receive only one gamma ray photon per second per square meter? Because there's a risk to other satellites being destroyed by the gamma rays from this satellite. So the flux which is the photons per area divided by time so this is the photons per area per time or photons per meters squared per second is the rate of photon production divided by the area over which those photons are going to be spread out and so we are going to assume that the photons are being spread out over a spherical surface at some distance r from the nuclear satellite and the area of this sphere will be 4π times radius squared so this r is the distance that the other satellite has to be away. So we can replace A with 4πr squared and then multiply both sides by r squared over flux per time and the flux per time cancels here and we are left with r squared on the left and on the right hand side, we have rate of photon production divided by 4π times the flux per time and take the square root of both sides to solve for r. So r then is the square root of 1.24844 times 10 to 13 photons per second divided by 4π times 1 photon per second per square meter and this works out to 9.967 times 10 to 5 meters or 997 kilometers.