Question
What is the wavelength of an electron accelerated through a 30.0-kV potential, as in a TV tube?
Final Answer
Solution video
OpenStax College Physics, Chapter 29, Problem 56 (Problems & Exercises)
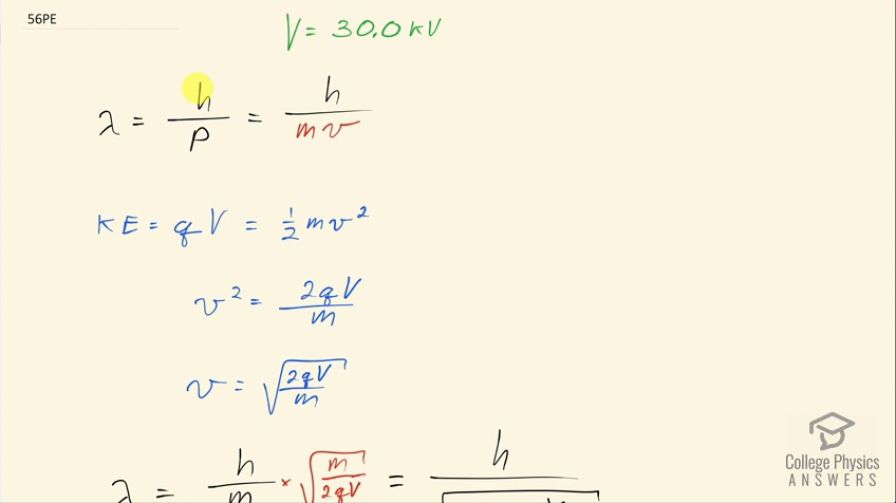
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. What is the wavelength of an electron that is accelerated through 30.0 kilovolts? The wavelength is Planck's constant divided by the momentum of the electron and momentum is the mass of the electron times its velocity and we'll figure out its velocity based on knowing its kinetic energy which will equal the charge on the electron multiplied by the potential difference through which it is accelerated so this is the drop in potential energy of the electron which will become its gain in electric energy and the other expression for kinetic energy is one-half mass times velocity squared. So we can solve this equation in blue for v squared by multiplying both sides by 2 over m and we end up with v squared then is 2qV over m and solving for v, we get by square rooting both sides and so v then is the square root of 2q times voltage divided by mass. We are going to substitute this in for v in this formula for wavelength but since we are dividing by this factor, we are going to multiply by the reciprocal of this fraction because I think it's confusing to have a fraction within a fraction so instead we'll flip this fraction over and multiply by it. So we have the square root of m over 2qV multiplied by h over m. This square root m divided by m becomes a square root m— factor in the denominator now— so we have h over square root 2 times charge times mass times voltage. That's 6.626 times 10 to the minus 34 joule seconds divided by square root of 2 times elementary charge times mass of an electron times 30.0 kilovolts written as 30.0 times 10 to the 3 volts and that is 7.08 times 10 to the minus 12 meters will be the electron's wavelength.
